| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionImg (inSeqImg) |
| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionImg (inSeqImg,params) |
| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionImg (inSeqImg,outImg) |
| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionMaskImg (inSeqImg,inOptSingleGreyMaskImg) |
| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionMaskImg (inSeqImg,params,inOptSingleGreyMaskImg) |
| outImg,eigenValues,eigenVectors,matrixRank = | pcaReductionMaskImg (inSeqImg,inOptSingleGreyMaskImg,outImg) |
Applies PCA to a sequence image to reduce its dimensionality.
The primary function of this algorithm is to reduce the temporal dimensionality of an input image (whose sequence elements are assumed to be 0-meaned and have a standard deviation of 1), while preserving the most significant part of information of it. To do that, first the image is reinterpreted as a matrix M with imgSizeC*imgSizeT rows and imgSizeX*imgSizeY*imgSizeZ columns. Each row is made of the pixel values of a sequence element of the input sequence of images.
A principal component analysis is then applied on this matrix M. It consists in:
- constructing the covariance matrix
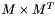 (square matrix of dimension
(square matrix of dimension 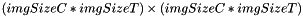 )
)
- computing the eigen vectors and eigen values on this covariance matrix
- keeping the eigen vectors that correspond to the largest eigen values (the principal components)
- projecting the initial image on these retained vectors to obtain the output image. The output image has the following property: its sequence elements are completely decorrelated.
The number of largest eigen values retained cannot exceed the number of rows of the matrix, ie. the temporal size multiplied by the number of color channels of the input image. There are several ways for the user to choose the number of the largest eigen values retained (ie. the temporal dimensionality of the output image), depending on the value of InOptPCAReductionParams attribute:
- if the parameter and the output image are left uninitialized, this number is initialized to the rank of the covariance matrix
- if the parameter is left uninitialized and if the output image is allocated by the user, this number is set to the temporal size of the output image
- if the parameter is initialized with the "number of expected sequence
elements" criterion, this number is set to the value specfied by the user
- if the parameter is initialized with the "variance threshold" criterion (see code example below), this number is set to the lowest number n of largest eigen values that satisfy the following formula:
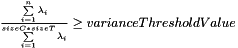 , assuming that
, assuming that 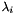 is the collection of eigen values sorted in decreasing order.
is the collection of eigen values sorted in decreasing order.
The different signatures of the 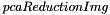 wrapper functions all return the results in a PCAReductionResults structure, that contains:
wrapper functions all return the results in a PCAReductionResults structure, that contains:
- the _pOutImg field, that contains the resulting reduced image
- the _pEigenValues field, that contains all the eigen values of the covariance matrix, sorted in decreasing order
- the _pEigenVectors field, that contains the corresponding eigen vectors (the ith element of the jth vector will be at position j * covariance_matrix_dimension + i in the collection)
- the _matrixRank field, that contains the rank of the covariance matrix
- Note
- It is possible to use only a subet of data, this is done by providing an additional mask image to the algorithm. In this case, the data where the mask equals True are used.
Example of Python code :
Example imports
import PyIPSDK
import PyIPSDK.IPSDKIPLClassification as classif
Code Example
inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
outImg, outEigenValues, outEigenVectors, outMatrixRank = classif.pcaReductionImg(inImg)
Example of C++ code :
Example informations
Header file
#include <IPSDKIPL/IPSDKIPLClassification/Processor/PCAReductionImg/PCAReductionImg.h>
Code Example
ImagePtr pOutImg = res._pOutImg;

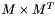 (square matrix of dimension
(square matrix of dimension 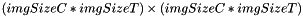 )
)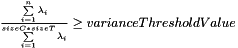 , assuming that
, assuming that 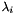 is the collection of eigen values sorted in decreasing order.
is the collection of eigen values sorted in decreasing order. wrapper functions all return the results in a PCAReductionResults structure, that contains:
wrapper functions all return the results in a PCAReductionResults structure, that contains: