GaussianNoiseStats = gaussianNoiseMsr (inImg)

Detailed Description

Estimation of measures of an additive zero-mean Gaussian noise.

For a given input image 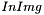$ InImg $ with an additive zero-mean Gaussian noise, the standard deviation is computed as follows :

$\sigma = \sqrt{\frac{\pi}{2}} \times \frac{1}{6 \times W \times H} \sum_{x = 1}^{W}{\sum_{y = 1}^{H}{\vert InImg(x, y) * M\vert}},$

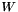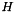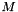where $W$ is the image width, $H$ is the image height, $ * $ is the convolution operator and $M$ is the difference of Laplacian mask kernel:

$M = 2 \left( L_1 - L_2 \right) = 2 \left( \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} 1 & 0 & 1 \\ 0 & -4 & 0 \\ 1 & 0 & 1 \end{bmatrix} \right) = \begin{bmatrix} 1 & -2 & 1 \\ -2 & 4 & -2 \\ 1 & -2 & 1 \end{bmatrix}$

See also: "Fast Noise Variance Estimation", J. Immerkaer, Computer Vision and Image Understanding, Vol. 64, pp. 300-302, 1996.

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLGlobalMeasure as glbmsr

Code Example

    # opening of input images
    image = PyIPSDK.loadTiffImageFile(inputImgPath)    
    
    # gaussian noise measurement
    gaussianNoiseMsrResult = glbmsr.gaussianNoiseMsr(image)
    
    # retrieve measurement results
    sigma = gaussianNoiseMsrResult.sigma

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLGlobalMeasure/Processor/GaussianNoiseMsr/GaussianNoiseMsr.h>

Code Example

        // compute statistic measures on input image
        GaussianNoiseStatsPtr pRes = gaussianNoiseMsr(pInImg);
        // retrieve associated results value
        const ipReal64 sigmaValue = pRes->getValue<GaussianNoiseStats::Sigma>();